Innovation Toy Model

R, Regression con términos de interacción

La innovación es uno de los pilares fundamentales para ser competitivos en la economía del conocimiento. En España, la innovación supone un porcentaje significativo de la cifra de negocios de las empresas. Sin embargo, se ha comprobado que el gasto empresarial en I+D financiado por el gobierno y los incentivos fiscales a la I+D representan un porcentaje bajo del PIB.

Por consiguiente, una sugerencia obvia para aumentar la competitividad nacional en la nueva economía es apostar por potenciar la innovación en las empresas. No obstante, para realizar la inversión de manera adecuada primero debe conocerse cómo responden los distintos tipos de empresas a las variaciones en el gasto dedicado a la innovación. Esto ayudará a conocer las empresas objetivo y a aproximar las cantidades de inversión más eficientes. Con estos objetivos en mente, se ha realizado un análisis de las empresas innovadoras para el período 2018-2020 en base al gasto que han dedicado a la innovación y según su tamaño mediante un modelo de regresión con interacciones.

Objetivos

Resultados

Modelo

Para responder a las cuestiones planteadas se ha elaborado un modelo económico partiendo de los datos referentes a I+D recogidos por el INE y la siguiente función de innovación:

$I_i = F(G_i,Z_i)$

Donde $I_i$ es el porcentaje de empresas innovadoras respecto a las empresas con gasto en innovación, $G_i$ el gasto en innovación y $Z_i$ una variable categórica según el tamaño de las empresas. $F(G_i,Z_i)$ se ha modelado como una función de producción no lineal.

$I_i=\alpha G_i^\beta Z_i^\delta\varepsilon$

Donde y son coeficientes es el término de error y una variable indicador. A continuación, se ha procedido a realizar la transformación logarítmica de la función de producción para obtener un modelo lineal.

$log(I_i)=\ \alpha+\beta\ log(G_i)+\delta\ log(Z_i)+\varepsilon_i$

A partir de este punto y para facilitar la nomenclatura vamos a asumir que las variables hacen referencia a su transformación logarítmica. Si desempaquetamos la variable indicador obtendremos:

$I_i=\ \alpha+\beta_1\ \delta_i^{Medianas}+\beta_2\delta_i^{Pequeñas}+\beta_3 G_i+\varepsilon_i$

Para extraer el máximo de información posible del modelo, vamos a incluir términos de interacción, los coeficientes de los cuales nos permitirán saber el diferencial de valor que tiene el gasto en inversión para un tipo de empresa u otra.

$I_i=\alpha+\beta_1\ \delta_i^{Medianas}+\beta_2\ \delta_i^{Pequeñas}+\beta_3 G_i+\beta_4 (G_i×\delta_i^{Medianas})+\beta5 (G_i×\delta_i^{Pequeñas})+\varepsilon_i$

El modelo ha obtenido un R² de 0.46 y los coeficientes estimados han sido los siguientes:

$I_i=3.55\ +0.94\delta_i^{Med}+1.8\delta_i^{Peq}+0.01G_i-0.07(G_i\times\delta_i^{Med})-0.12(G_i\times\delta_i^{Peq})+\varepsilon_i$

Análises de coeficientes

A partir de la ecuación anterior se pueden observar las diferencias en el efecto del gasto para los distintos tipos de empresas. Para las empresas medianas, el efecto del gasto será 0.07 puntos menor que para las grandes. En el caso de las empresas pequeñas, será 0.12 puntos menor.

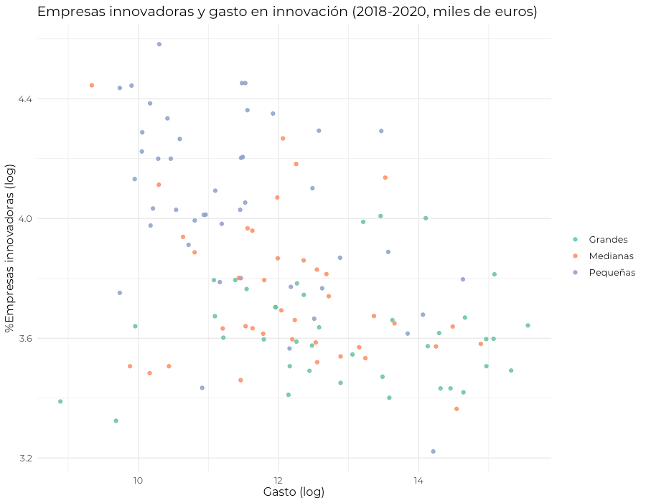
A continuación, puede observarse un gráfico de gasto-innovación donde cada punto representa el conjunto de empresas según su tamaño en un sector determinado, junto con las líneas de regresión estimadas.

Si lo examinamos, podemos ver como son los grupos de pymes los que cuentas con un mayor número relativo de empresas innovadoras a pesar de contar con un gasto menor en innovación. No obstante, el modelo predice, para estas, una tendencia decreciente a medida que aumenta el gasto que es importante estudiar.

Análises de derivadas parciales

Si calculamos las derivadas parciales del modelo lineal, obtendremos las siguientes ecuaciones. Su interpretación puede resultar especialmente útil para extraer conclusiones sobre el modelo.

$\frac{\partial I_i}{\partial G_i}=0.01-0.07\delta_i^{Med}-0.12\delta_i^{Peq}$

La primera ecuación nos informa del valor esperado de innovación dado un incremento en el gasto. Es decir, cómo evolucionará en promedio el porcentaje de empresas innovadoras si aumenta el gasto. Para las empresas medianas obtenemos un valor de -0.06, para las pequeñas de -0.11 y para las grandes de 0.01. Esto quiere decir que, si aumentáramos continuamente la inversión en innovación destinada a empresas, a la larga, tan solo las grandes empresas conseguirían mejorar su sistema de innovación y, aun así, su sensibilidad a los incrementos sería bastante limitada.

$\frac{\partial I_i}{\partial\delta_i^{Med}}=0.94-0.07G_i$

La segunda ecuación aporta información sobre el comportamiento de la innovación en relación con el gasto para los grupos de empresas medianas. Nos informa de que el valor esperado de innovación para las empresas medianas será 0.94 puntos mayor que para las grandes. Sin embargo, los incrementos en el gasto van mermando esta ventaja inicial, que desaparecerá para un gasto igual a unos 680,103.3 miles de euros y pasará a ser negativa para importes superiores.

$\frac{\partial I_i}{\partial\delta_i^{Peq}}=1.8-0.12G_i$

La tercera ecuación aporta la misma información que la segunda, pero para el caso de las empresas pequeñas. Nos informa de que el valor esperado de innovación para las pequeñas empresas será 1.8 puntos mayor que para las grandes. No obstante, al igual que con las empresas medianas, al aumentar el gasto esta ventaja irá desapareciendo hasta volverse nula para un gasto igual a 3,269,017 miles de euros y pasará a ser negativa para importes superiores.

Conclusiones

• Las pymes tienen un valor esperado de innovación mayor que las grandes empresas, especialmente las empresas pequeñas.
• La ventaja innovadora de las pymes desaparece cuando el gasto supera un cierto umbral (680,103.3 m€ para el conjunto de empresas medianas por sector y 3,269,017m€ para el de empresas pequeñas).
• Una posible explicación para este fenómeno sería que las pymes son incapaces de gestionar de forma eficiente inversiones demasiado elevadas en innovación. El menor coeficiente asociado al gasto para las empresas pequeñas en comparación con las medianas refuerza esta idea, ya que nos comunica que cuanto menor es el tamaño de las empresas, más difícil resulta la gestión del gasto. Sin embargo, otra posibilidad es que el modelo incluya efectos que dependen del sector productivo, pudiendo haber sectores más o menos eficientes a la hora de transformar el gasto en innovación.
• Finalmente, se debe concluir con un mensaje de advertencia. El modelo presenta una visión simplificada del panorama económico. Por ejemplo, no captura los efectos que dependen del sector productivo. Sin embargo, los hallazgos que sugiere este toy model hablan sobre la importancia de realizar un estudio más detallado sobre el tema.